Game Theory in Quantitative Techniques: A Powerful Tool for Decision-Making in 2025

Related Articles: Game Theory in Quantitative Techniques: A Powerful Tool for Decision-Making in 2025

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Game Theory in Quantitative Techniques: A Powerful Tool for Decision-Making in 2025. Let’s weave interesting information and offer fresh perspectives to the readers.

Game Theory in Quantitative Techniques: A Powerful Tool for Decision-Making in 2025

Game theory, a branch of mathematics concerned with strategic decision-making in situations of interdependence, is increasingly finding its place within the realm of quantitative techniques. As we approach 2025, its influence is set to become even more pronounced, particularly in fields like finance, economics, and artificial intelligence. This article explores the key aspects of game theory, its potential applications in quantitative techniques, and its significant contributions to solving complex decision problems.

Understanding the Fundamentals of Game Theory

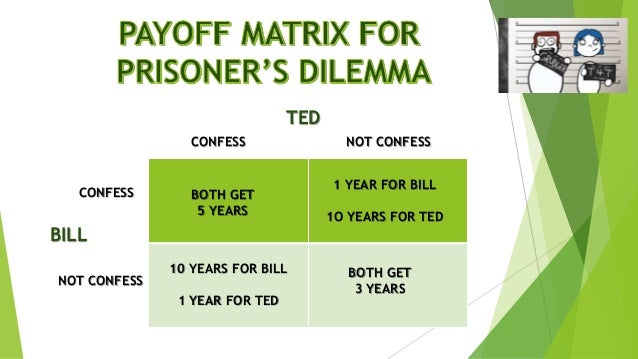
At its core, game theory explores scenarios where multiple individuals or entities, known as players, interact strategically. Each player aims to maximize their own payoff, considering the actions and potential responses of other players. This interplay of strategic choices and potential outcomes forms the foundation of game theory.

The basic elements of a game include:

• Players: The individuals or entities making decisions.
• Strategies: The set of actions available to each player.
• Payoff: The outcome or reward associated with each player’s strategy, given the actions of other players.
• Information: The level of knowledge each player has about the game, including the strategies of other players.

Key Concepts in Game Theory

Several fundamental concepts within game theory provide valuable insights into strategic interactions:

• Nash Equilibrium: A state where no player can improve their payoff by unilaterally changing their strategy, given the strategies of other players. This signifies a stable point in the game, where no player has an incentive to deviate.
• Dominant Strategy: A strategy that yields the highest payoff for a player regardless of the actions of other players. If a dominant strategy exists, it is generally the optimal choice for the player.
• Mixed Strategy: A probabilistic approach where a player chooses between different strategies with a certain probability. This helps to counter predictable patterns and introduce uncertainty into the game.
• Zero-Sum Game: A scenario where the gains of one player equal the losses of another. In such games, there is a fixed amount of resources to be divided, creating a competitive dynamic.
• Non-Zero-Sum Game: A game where players can achieve positive outcomes simultaneously, emphasizing cooperation and collaboration.

Applications of Game Theory in Quantitative Techniques

The principles of game theory are increasingly employed in quantitative techniques across various disciplines, providing valuable tools for analysis and decision-making. Some prominent applications include:

• Finance: Game theory is used to model market behavior, analyze investment strategies, and understand the dynamics of financial markets. It helps to assess risks, anticipate market trends, and optimize portfolio allocation.
• Economics: Game theory is instrumental in understanding economic interactions, including competition among firms, consumer behavior, and government policy. It provides insights into pricing strategies, market equilibrium, and the impact of regulatory interventions.
• Artificial Intelligence (AI): Game theory plays a crucial role in the development of intelligent agents, enabling them to make strategic decisions in complex environments. It is used in areas like multi-agent systems, game playing, and automated negotiation.
• Operations Research: Game theory aids in optimizing resource allocation, scheduling, and logistics. It helps to determine the best course of action in situations where multiple parties compete for limited resources.
• Political Science: Game theory is employed to analyze political strategies, understand voting behavior, and model international relations. It provides insights into coalition formation, power dynamics, and conflict resolution.

Game Theory in Quantitative Techniques 2025: A Look Ahead

As we move towards 2025, the application of game theory in quantitative techniques is poised to expand further, driven by advancements in computing power, data analysis, and the increasing complexity of decision-making environments.

• Evolutionary Game Theory: This branch of game theory explores the evolution of strategies over time, considering factors like learning, adaptation, and population dynamics. It is gaining importance in fields like economics, biology, and social sciences, where long-term strategic interactions are crucial.
• Mechanism Design: This area focuses on designing rules and incentives to achieve desired outcomes in strategic settings. It is becoming increasingly relevant in areas like online marketplaces, auctions, and decentralized systems, where effective mechanisms are crucial for efficient resource allocation and fair competition.
• Game Theory in AI: The integration of game theory with AI is rapidly evolving, leading to the development of more sophisticated and intelligent agents capable of navigating complex decision-making scenarios. This includes areas like adversarial machine learning, where agents compete against each other to achieve their goals.
• Big Data and Game Theory: The availability of massive datasets presents new opportunities for applying game theory to analyze complex patterns, predict future outcomes, and optimize decision-making processes. This is particularly relevant in fields like finance, marketing, and social sciences, where understanding large-scale interactions is crucial.

FAQs by Game Theory in Quantitative Techniques 2025

Q: What are the limitations of game theory?

A: While game theory offers powerful tools for analyzing strategic interactions, it has limitations. It often relies on simplifying assumptions about player rationality, complete information, and static environments. In real-world scenarios, players may act irrationally, possess incomplete information, or operate in dynamic environments, which can limit the applicability of game theory.

Q: How can game theory be used to solve real-world problems?

A: Game theory can be applied to solve various real-world problems, such as:

• Pricing strategies: Firms can use game theory to determine optimal pricing strategies, considering the competitive landscape and consumer behavior.
• Negotiation: Game theory can assist in negotiation processes by understanding the interests and preferences of different parties, leading to more efficient and mutually beneficial outcomes.
• Resource allocation: Game theory can optimize resource allocation in situations where multiple parties compete for limited resources, such as in environmental management or disaster relief.

Q: What are some ethical considerations associated with game theory?

A: The use of game theory raises ethical concerns, particularly when applied to situations involving power imbalances or potential for manipulation. It is crucial to ensure that the application of game theory is fair, transparent, and does not exploit or disadvantage any party.

Tips by Game Theory in Quantitative Techniques 2025

• Identify the key players: Clearly define the individuals or entities involved in the strategic interaction.
• Define the strategies: Identify the possible actions available to each player.
• Determine the payoffs: Assign numerical values to the outcomes associated with different combinations of strategies.
• Consider the information available: Analyze the level of knowledge each player has about the game and the strategies of others.
• Apply appropriate game theory concepts: Choose the relevant concepts and models based on the specific characteristics of the game.

Conclusion by Game Theory in Quantitative Techniques 2025

Game theory is a powerful tool for understanding and solving complex decision-making problems in various fields. Its applications in quantitative techniques are expanding rapidly, driven by advancements in computing power, data analysis, and the increasing complexity of strategic interactions. As we move towards 2025, game theory is poised to play an even more significant role in shaping our understanding of strategic decision-making and guiding us towards optimal solutions in a world increasingly characterized by interdependence and complexity. By embracing the principles and applications of game theory, we can navigate these challenges more effectively and achieve better outcomes in our individual and collective endeavors.

Closure

Thus, we hope this article has provided valuable insights into Game Theory in Quantitative Techniques: A Powerful Tool for Decision-Making in 2025. We thank you for taking the time to read this article. See you in our next article!